Consider the sequence
1, -3, 9, -27, 81, -243
The terms of the sequence alternate between positive and negative numbers.
The base is the above expressions is -3.
To solve the equation
with
we can log both sides to obtain
(1) (log here means log base 10 )
This is not a general result for real numbers. It can only be used for
since we cannot take the log of a negative number (at least when keeping to real numbers).
If we try and solve it for the equation
applying (1) we obtain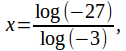
which is not defined, since the log of a negative number is not defined (keeping to real numbers). In fact, inspection of the equation
returns the solution
We can however solve the equation by taking log base (-3) of both sides. If we do this for the equation
we obtain
Now use the identity
if
to give
to give
This method works in this particular case, but not generally.
The equation
has no solution in real numbers with any amount of manipulation. Solutions involving complex numbers do exist however.