The change of base rule is one of the laws of logarithms and allows us to change the base of a logarithm. It states
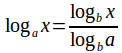
We can prove this formula for the change of base rule stating from the equation
(1)
Raising
to the poswer of both sides gives
Now take log base b of both sides to give
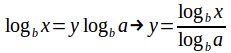
Finally use (1) to give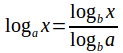
Notice that if
then this becomes
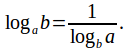
The change of base rule is sometimes useful to solve log equations with more than one log when the bases of the logs are not the same.
Example: Solve the equation
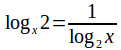so this equation becomes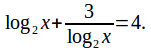
Substitute
to obtain
and rarrange to give
We can factorise this expression to give
and solve it to give
If
If