The backwards form of the trangle inequality states that for any two vectors
and
The meaning of the theorem is shown in the following diagram.
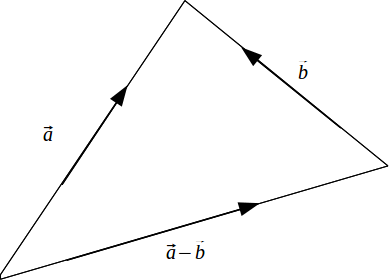
We can also illustrate with real numbers, which may be considered one dimensional vectors.
Take
and
The proof follows from the dot product of
with itself.
Square rooting both sides now gives