The speed of a plane is usually quoted in still air. In fact, air is never still. There is always a small amount of wind. This is significant for airplanes that must navigate for hundreds or thousands of miles, ensuring that they arrive at the destination safely, having used the minimum amount of fuel. Aircraft take account of the wind when flying in a straight line between start and destination airports by pointing air relative to the wind so that a straight line is mauintained. Since the wind is flowing past the plane, the effective speed of the plane – the groundspeed – will also be changed. A worked example of the calculations they must make is described below.
A plane has a speed of 400 km/h in still air. It is to fly to an airport on a bearing of 045° when the airspeed is 20 km/h on a bearing of 330°. Find the direction the pilot must fly the plane and the speed of the plane relative to the ground.
As shown on the diagram below, the pilot must steer the plane into the wind slightly to follow the correct path over the ground.
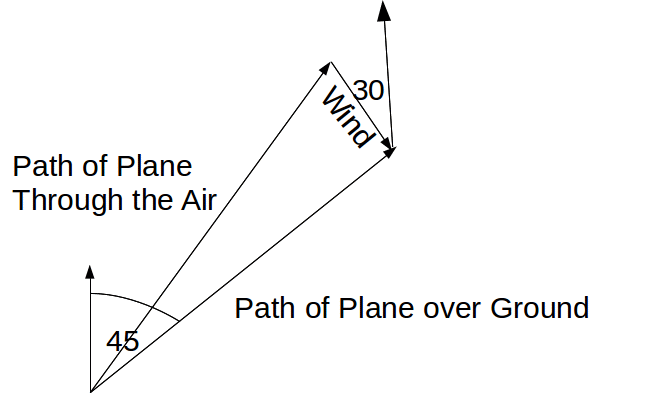
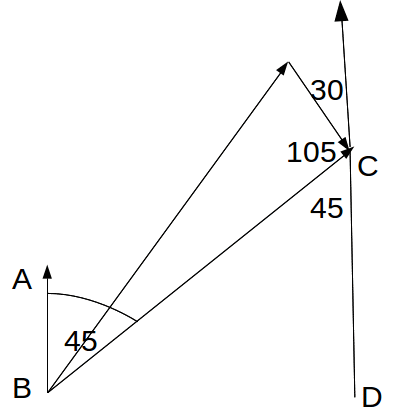
We can find an angle in the triangle by drawing in am extra line, as shown below. ABCD is a Z shape with Ab parallel to DC so angle ABC= angme BCD then the angle in the trangle at C is 190-(45+30)=105°.
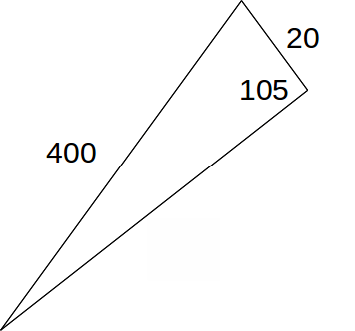
Marking the speeds of the palne and wind on the diagram gives us the diagram below.
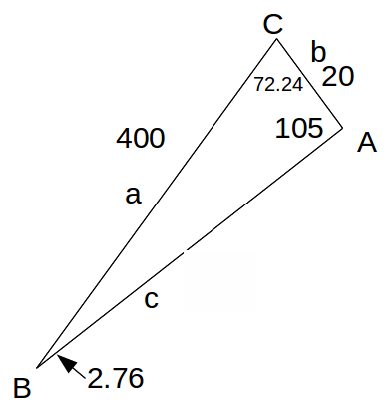
We can now find the speed of the plane over the ground and the bearing using the sine and cosine rules. Label the sides and angles of the triangle as below.
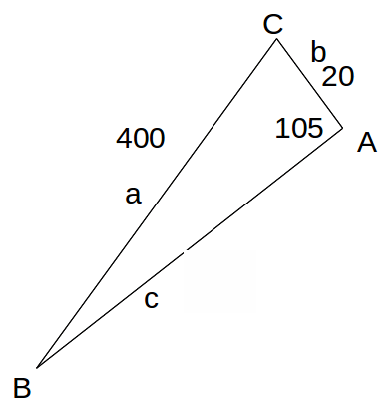
From the Sine Rule,![]()
The bearing is then 45°-2.76°=042.24°. Angle C is then 180°-105°-2.76°=72.24°.
The Cosine Rule then states![]()
