Finding the point of Intersection of Two Lines in Three Dimensions

If two lines intersect, they are both in the same place at the same time, so to speak. We don't know what the point is, but because they both meet at the same point, we can put the equations of the lines equal to each other. This will result in simultaneous equations for the parameters. We solve them, then substitute back in to the lines to find the point.

Example: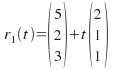and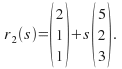Find if the lines intersect and if they do intersect, find the coordinates of the point of intersection.

Put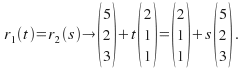

Put each component ofequal to the corresponding component ofWe obtain

(1)

(2)

(3)

(2)-(3) gives

Substituteinto (1), (2) or (3) to give t=1.

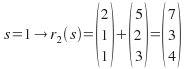and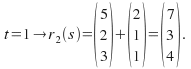

Hence both equations meet at the same pointwhen

If the lines do not intersect at a point then the two points will not be the same or equivalently there will not be values of s ant t that satisfy all three equations simultaneously.

Example: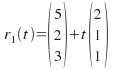and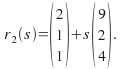

We form the same equations as before and perform (2)-(3) to getbut equation (1) is nowanddo not satisfy this equation so these lines do not intersect.