\[\vec{a} , \: \vec{b}\]
.The area of the parallelogram is the magnitude of the cross or vector product of the vectors
\[\| \vec{a} \times \vec{b} \| = \| \vec{a} \| \| \vec{b} \| sin \theta\]
where \[\theta\]
is the angle between \[\vec{a}\]
and \[\vec{b}\]
.The cross product is itself a vector, perpendicular to both
\[\vec{a}\]
and \[\vec{b}\]
but the area is equal to the magnitude.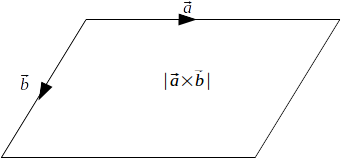
\[\vec{a} , \: \vec{b}\]
is half the area of the parallelogram \[\frac{1}{2} \| \vec{a} \| \| \vec{b} \| sin \theta\]
. 