The basic relationship that expresses random decay as a random process is sxpressed mathematically as
where N is the number of undecayed atoms remaining.
The constant of proportionality is negative since N is decreasing so dN < 0. We may write
where
is the number of decays in each time period
typically taken to be 1 second, and
is a positive constant called the decay constant. The proportion of atoms that will decay in a time dt or probability that an individual atom will decay in a time
is then
We can solve the equation
obtaining
where N-0 is the number of undecayed atoms initially present. A similar expression exists for the activity
We can find the decay constant %lambda in the following way.
Take natural logarithms ofobtaining
This is the equation of a straight line graph, with
on the vertical axis and gradient
A graph of N against t is shown below. The number of undecayed atoms fall by a half in each fixed time period called the half life, labelled
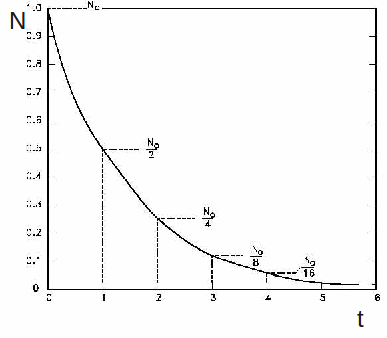
We can find the half life by substituting
and
into 
Alternatively we could observe the time taken for the activity to decay by a half, but this is less accurate.