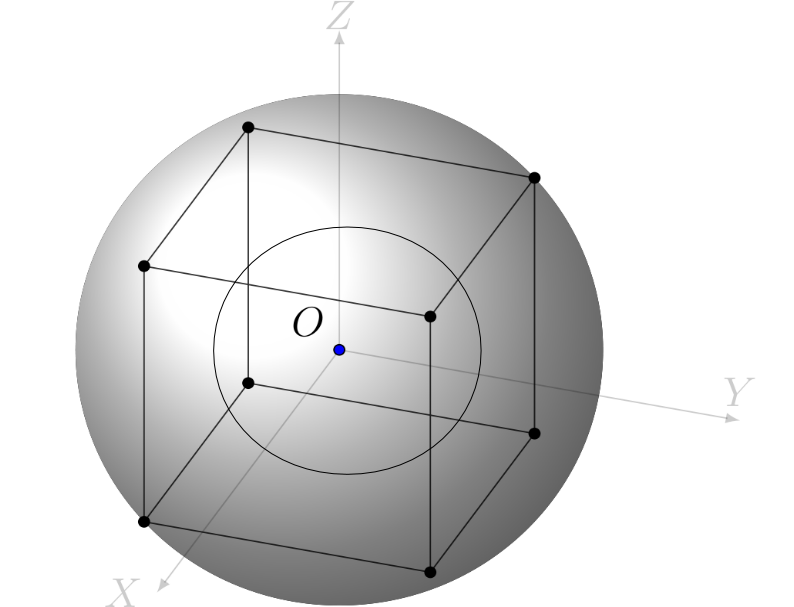
\[2x\]
the the innermost sphere has radius \[x\]
.The radius of the larger sphere is the distance from the centre of the cube to one of its vertices, and is equal to
\[\sqrt{x^2+x^2+x^2} = \sqrt{3x^2} = x \sqrt{3}\]
Then
\[\frac{Volume \: of \: Large \: Sphere}{Volume \: of \: Small \: Sphere}= \frac{4/3 \pi (x \sqrt{3})^3}{4/3 \pi x^3} = 3 \sqrt{3}\]
