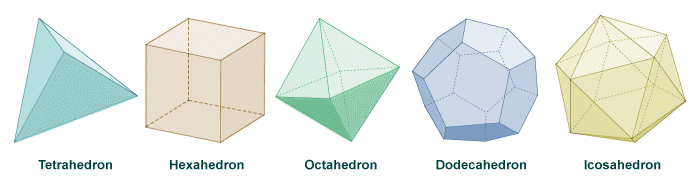
On - the cuber - can be made from 6 squares.
The Dodecahedron can be made from 12 pentagons.
There can be no more such solids, because for
\[n>5\]
the interior angle is \[\frac{180(n-2)}{n}\]
and 360 divides by this number \[\frac{360}{180(n-2)/n} = \frac{2n}{n-2}\]
must be at least 3 or we have have just two shapes at a point and would not fold the plane up and fit another shape in the gap. If \[n=6\]
then \[\frac{2n}{n-2}\]
is exactly 3 and the 6 sided shapes are regular hexagons. We can tile the plane with regular hexagons, but can not fold the plane up while keeping the hexagons flat to make a solid.