Suppose we have an isosceles triangle with base given, and a circle inscribed inside it, of given radius.
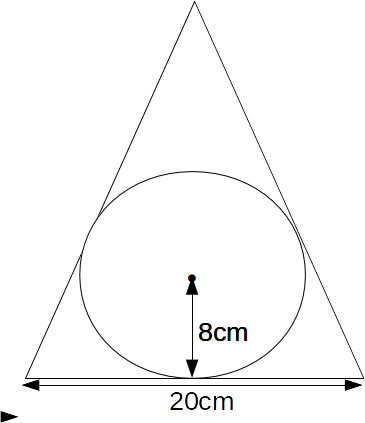
We can calculate the height of the triangle.,
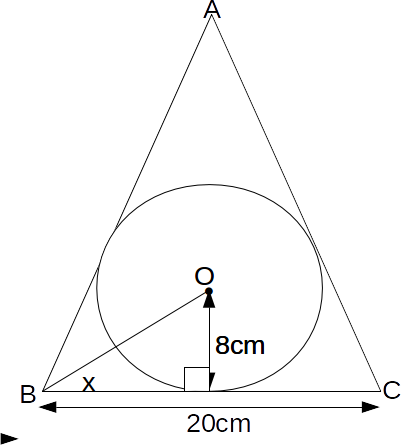
Label the Vertices of the triangle A, B and C and draw a line from the centre of the circle to B. The angle
\[x= tan^{-1}(8/10)=38.66 \deg\]
.
Draw a line from the centre of the circle to the side AB, which meets the side at P.
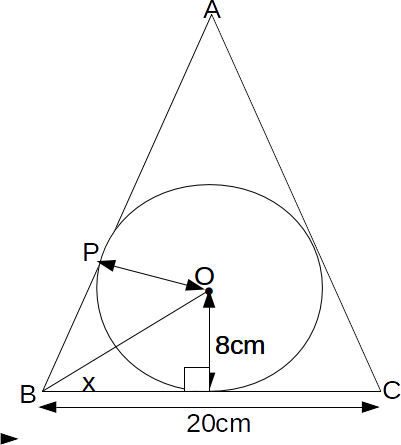
The two triangles so far construct, have the side OB in common, correspond equal side, equal to the radius of the circle, and corresponding equal angles (right angles), so angle
\[APO=x\]
and angle
\[ABC=2x= 77.32 \deg\]
.
Now construct another right angled triangle as shown.
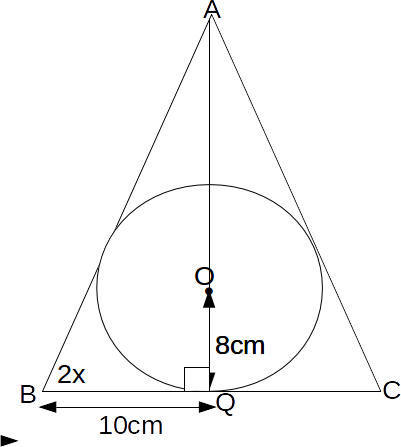
The height of the triangle is then
\[AQ tan (2x)=44.44 cm\]




