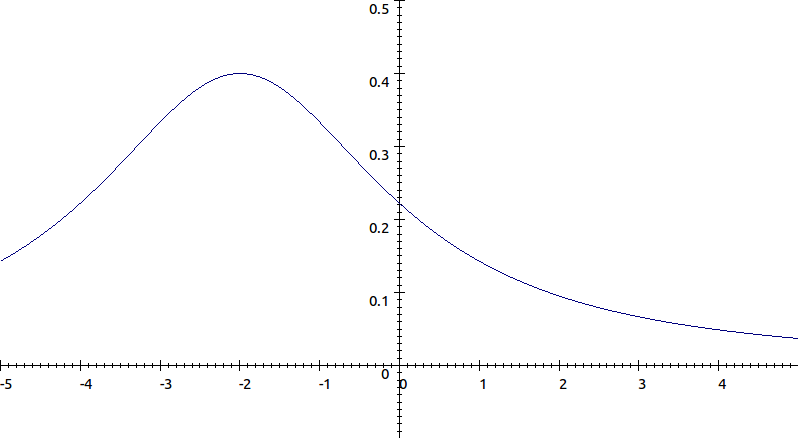
Suppose we want to find the bounds of
\[\frac{2}{x^2+4x+9}\]
.Numerator and denominator are both positive, and as
\[x \rightarrow \infty 0\]
, the denominator tends to infinity also, so the fraction tends to zero. Hence \[0 \lt \frac{2}{x^2+4x+9}\]
.Completing the square for the denominator gives
\[\frac{2}{x^2+4x+9}=\frac{2}{(x+2)^2+5}\]
.To maximise this fraction we must minimise the denominator, which is the sum of non negative terms. The denominator is minimised when
\[(x+2)^2=0 \rightarrow x=-2\]
.For this value of
\[x\]
the fraction is equal to \[0 \lt \frac{2}{(-2+2)^2+5}=\frac{2}{0+5}=\frac{2}{5}\]
.Hence
\[0 \lt \frac{2}{x^2+4x+9} \lt \frac{2}{5}\]
.The graph of the function is shown below.