In general a quadratic curve may have one, two or no roots, as shown.
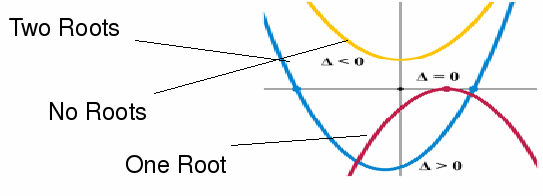
For the curve
the number of roots depends entirely on the discriminant
If
there are no roots.
If
there is one root.
If
there are two roots.
We are typically asked: Find the set of values of
for which the curve
has
no roots:
always, for every value of
so for every value of k the curve has two roots.
Example: Find the set of values offor which the curve
has two roots.
We solve for
So solutions exist for all values of
Example: Find the set of values offor which the curve
has one root.
We solve for
So
or