\[h\]
slant height \[l\]
and base radius \[r\]
is \[A=\pi rl\]
.A frustum is a truncated cone. Part of the top is cut off by a cut parallel to the base.
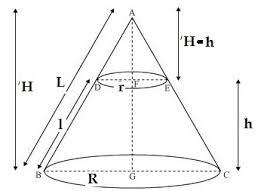
\[\frac{L-l}{r}=\frac{L}{R} \rightarrow LR-lR=Lr \rightarrow L=\frac{lR}{R-r}\]
and \[L-l=\frac{lR}{R-r}-l=\frac{lR-lR+lr}{R-r}=\frac{lr}{R-r}\]
.The surface area of the frustum is then
\[\begin{equation} \begin{aligned} A_{FRUSTUM}&=\pi RL-\pi r(L-l) \\ &=\pi (R \frac{lR}{R-r} -r \frac{lr}{R-r} ) \\ &=\frac{\pi l}{(R-r)}(R^2-r^2) \\ &= \frac{\pi l}{(R-r)}(R-r)(R+r)= \pi l(R+r)\end{aligned} \end{equation}\]
