Simultaneous equations usually refers to equations of the form
(1)
(2)
We solve these be equating the coefficients of
or 
and then eliminating that term. For example, in this case we can multiply (1) by 3 to get
then subtract (2)
and from (1),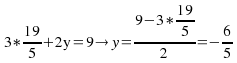
Our problem here is to solve equations such as
(1)
(2)
The general approach is to rearrange the linear equation (2) to make the subject say, then substitute the rearranged equation into the quadratic to find a quadratic equation inwhich we solve to findthen substitute back into the linear equation to find
For the above example:
Replace the
in with 
to get
We expand the brackets and simplify this expression:
We can factorise and solve the last expression.
If
we use (2) to find
and if
we use (1) to find
Example:
(1)
(2)
Make the subject of (2), then substitute the rearranged equation into (1) to find a quadratic equation inwhich we solve to findthen substitute this into the (2) to find
Replace thein 
with 
to get
We expand the brackets and simplify this expression:
If 
we use (2) to find
and if
we use (1) to find