The Hamiltonian![]() represents the energy of the system which is the sum of kinetic and potential energy, labelled
represents the energy of the system which is the sum of kinetic and potential energy, labelled![]() and
and![]() respectively. For a one dimensional system, we may write
respectively. For a one dimensional system, we may write
![]() so
so![]()
where![]() Note that
Note that![]() is a function of
is a function of![]() only and
only and![]() is a function of
is a function of![]() only. In general
only. In general![]() is a function of
is a function of![]() only and
only and![]() is a function of the coordinates, however they are defined.
is a function of the coordinates, however they are defined.
The value of the Hamiltonian is the total energy of the system. For a closed system, it is the sum of the kinetic and potential energy in the system and is conserved. The Hamiltonian equations give the time evolution of the system. These are
![]() where
where![]() and
and![]()
The time-derivative of the momentum![]() equals the force acting so the first Hamilton equation means that the force on the particle equals the rate at which it loses potential energy with respect to changes in
equals the force acting so the first Hamilton equation means that the force on the particle equals the rate at which it loses potential energy with respect to changes in![]() its position.
its position.
The time-derivative of![]() here means the velocity: the second Hamilton equation here means that the particle’s velocity equals the derivative of its kinetic energy with respect to its momentum.
here means the velocity: the second Hamilton equation here means that the particle’s velocity equals the derivative of its kinetic energy with respect to its momentum.
We can derive Hamilton's equations by looking at how the total differential of the Lagrangian depends on time, generalized positions![]() and generalized velocities
and generalized velocities![]()
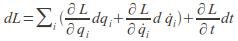 (1)
(1) - Now use
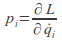 and
and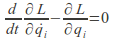 to give
to give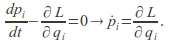
Substitute these into (1):![]() which we can rewrite as
which we can rewrite as![]() and rearrange to get
and rearrange to get![]()
The term on the left-hand side is the Hamiltonian so
![]()
where the second equality holds because it is equal to![]() Associating terms from both sides of the equation above yields Hamilton's equations
Associating terms from both sides of the equation above yields Hamilton's equations
![]() and
and![]()
