The function![]() which is a solution to Laplace's or Posson's equation and satisfies the boundary conditions is the only function which has these properties, because it is found by integrating Laplace's or Poisson's equation in a methodical manner. Unfortunately for a general distribution of charge, systematic integration is not possible. However suppose that in some region we have found a solution that satisfies the boundary conditions. Then this is the only possible solution.
which is a solution to Laplace's or Posson's equation and satisfies the boundary conditions is the only function which has these properties, because it is found by integrating Laplace's or Poisson's equation in a methodical manner. Unfortunately for a general distribution of charge, systematic integration is not possible. However suppose that in some region we have found a solution that satisfies the boundary conditions. Then this is the only possible solution.
The uniqueness of the solution for Laplace's equation is easy to prove by considering the potential inside a cavity in a piece of conducting material. The potential on the boundary of the cavity is constant,![]() say. If there is no charge in the cavity, the potential inside it must obey Laplace's equation,
say. If there is no charge in the cavity, the potential inside it must obey Laplace's equation,![]() One solution of this equation is
One solution of this equation is![]() throughout the cavity. This is the only solution, for if there were another, say
throughout the cavity. This is the only solution, for if there were another, say![]() then
then![]() must have a minimum or maximum inside the cavity since
must have a minimum or maximum inside the cavity since![]() on the walls but there must be at least one point where
on the walls but there must be at least one point where![]() But solutions of Laplace's equation cannot have minima or maxima. At a maxima for example,
But solutions of Laplace's equation cannot have minima or maxima. At a maxima for example,![]() see diagram below
see diagram below
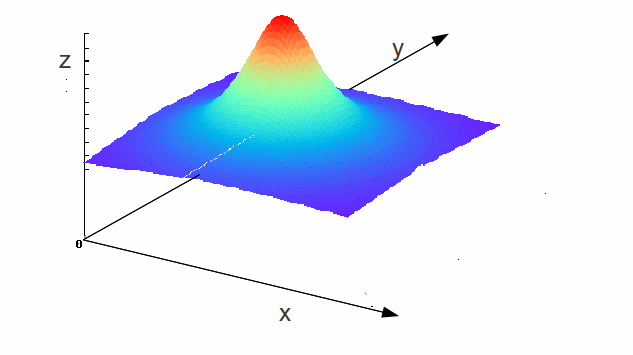
which illustrates why![]() and
and![]() in two dimensions, with an obvious extension to three dimensions - but this contradicts that
in two dimensions, with an obvious extension to three dimensions - but this contradicts that![]()
The uniquess theorem for Poisson's equation can be proved by assuming that![]() and
and![]() are both solutions with the same boundary values. The difference
are both solutions with the same boundary values. The difference![]() must be zero on the boundary and must satisfy Laplace's equation everywhere. One solution to Laplace's equation with
must be zero on the boundary and must satisfy Laplace's equation everywhere. One solution to Laplace's equation with![]() on the boundary is
on the boundary is![]() everywhere and this is the only possible solution. It follows that there cannot be two solution
everywhere and this is the only possible solution. It follows that there cannot be two solution![]() and
and![]() satisfying the same boundary conditions and the uniqueness theorem holds for Poisson's equation too.
satisfying the same boundary conditions and the uniqueness theorem holds for Poisson's equation too.
