\[V_R\]
.The voltage drop across a capacitor is
\[V_C=\frac{Q}{C}= \frac{1}{C} \int I dt\]
.The voltage drop across an inductor is
\[V_L=L \frac{dI}{dt}\]
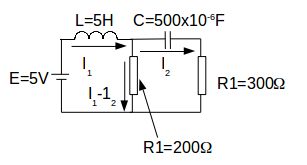
.Using Kirchoff's Law for the left hand loop gives
\[E-V_L-V_{R_1}=0\]
. (1)The voltages across the resistor and inductor respectively are
\[V_{R_1}=R_1(I_1-I_2), , \: V_L=L \frac{dI_1}{dt}\]
. Substituting these into (1) gives \[E- L \frac{dI_1}{dt}-R(I_1-I_2)=0\]
.Hence
\[50- 0.5 \frac{dI_1}{dt}-200(I_1-I_2)=0\]
. (2)Applying Kirchoff's Voltage Law to the right hand loop
\[V_R+V_C+V_{R_2}\]
hence \[\frac{1}{C} \int I_2 dt+I_2R_2+R_1(I_1-I_2)=0 \rightarrow \frac{1}{C} \int I_2 dt-R_1I_1+I_2(R_1+R_2)=0\]
.Let
\[Q=\frac{dI_2}{dt}\]
and \[I_2=\frac{dQ}{dt}\]
.\[ \frac{Q}{C}-R_1I_1+\frac{dQ}{dt}(R_1+R_2)=0\]
.Using the values from the diagram gives
\[ \frac{1}{50 \times 10^{-6}} \int I_2 dt-200I_1+500 \frac{dQ}{dt}=0 \rightarrow \frac{dQ}{dt}-0.4I_1+40Q=0 \rightarrow \frac{dQ}{dt}=-40Q+0.4I_1\]
. (3)Use
\[I_2=\frac{dQ}{dt}\]
in (2) to give \[50- 0.5 \frac{dI_1}{dt}-200(I_1-\frac{dQ}{dt})=0 \rightarrow 50-0.5 \frac{dI_1}{dt}-200I_1+200 \frac{dQ}{dt}=0\]
.Substitution of (3) into the last equation results in the equation
\[50-0.5 \frac{dI_1}{dt}-120I_1+80Q=0 \rightarrow \frac{dI_1}{dt}=-240I_1+1600Q+100\]
.We now have the equations
\[\frac{dQ}{dt}=-40Q+0.4I_1\]
\[\frac{dI_1}{dt}=-240I_1+1600Q+100\]
We can write this in matrix form as
\[\begin{pmatrix} \frac{dI_1}{dt}\\ \frac{dQ}{dt}\end{pmatrix} = \left( \begin{array}{ccc} -240 & -1600 \\ 0.4 & -40 \end{array} \right) \begin{pmatrix} I_1\\ Q \end{pmatrix} + \begin{pmatrix} 100 \\ 0\end{pmatrix}\]
The eigenvalues and eigenvectors are
\[\lambda_1=-80, \: \lambda_2=-200\]
, \[\mathbf{v}_1 = \begin{pmatrix}-100\\1\end{pmatrix}, \: \mathbf{v}_2 = \begin{pmatrix}-400\\1\end{pmatrix}\]
.The solution to the homogeneous system is then
\[\begin{pmatrix} I_1\\ Q \end{pmatrix}=Ae^{-80t}\begin{pmatrix}-100\\1\end{pmatrix}+Be^{200t}\begin{pmatrix}-400\\1\end{pmatrix} \]
.To find a particular solution, assume
\[\frac{dI_1}{dt}=\frac{dQ}{dt}=0\]
. Then
\[0=-240I_1-1600Q+100\]
.\[0=0.4I_1-40Q\]
We get
\[I_1=1/4, \: Q=1/400\]
The general solution is then
\[\begin{pmatrix} I_1\\ Q \end{pmatrix}=Ae^{-80t}\begin{pmatrix}-100\\1\end{pmatrix}+Be^{200t}\begin{pmatrix}-400\\1\end{pmatrix}+\begin{pmatrix}1/4\\1/400\end{pmatrix} \]
.This can be fitted to any initial conditions.
