Frequencies of Laddered LC Circuits
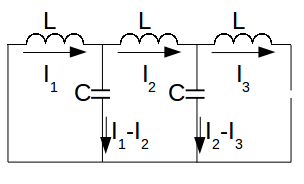
\[V_L\]
across an inductance \[L\]
is given by \[V_L = L \frac{dI}{dt}\]
and the voltage \[V_C\]
across a ca[capacitance \[C\]
holding a charge \[Q\]
is given by \[V_C =\frac{Q}{C}\]
.Since there is no battery or power supply in the circuit,
\[L \frac{dI_1}{dt}+\frac{Q_1}{C}=0\]
by Kirchoff's Voltage Law.Differentiation gives
\[L \frac{d^2I_1}{dt^2}+\frac{1}{C}\frac{dQ_1}{dt}=0\]
But
\[\frac{dQ_1}{dt}=I_1-I_2\]
so \[L \frac{d^2I_1}{dt^2}+\frac{I_1}{C}-\frac{I_2}{C}=0 \rightarrow L \frac{d^2I_1}{dt^2}=-\frac{I_1}{C}+\frac{I_2}{C}\]
.Similarly for the second and third loops.
\[L \frac{d^2I_2}{dt^2}=\frac{I_1}{C}-2\frac{I_2}{C}+\frac{I_3}{C}\]
.
\[L \frac{d^2I_3}{dt^2}=\frac{I_2}{C}-\frac{I_3}{C}\]
.In simple LC circuits with a battery or power supply, current is periodic and simple harmonic, like a mass spring system. Hence
\[ \frac{d^2I_1}{dt^2}=-\omega_1^2 I_1, \: \frac{d^2I_2}{dt^2}=-\omega_2^2 I_2, \: \frac{d^2I_3}{dt^2}=-\omega_3^2 I_3\]
.The differential equations become
\[L \omega^2 I_1 =-\frac{I_1}{C}+\frac{I_2}{C}\]
\[L \omega^2 I_2 =\frac{I_1}{C}-2\frac{I_2}{C}+\frac{I_3}{C}{C}\]
\[L \omega^3 I_3 =\frac{I_2}{C}-\frac{I_3}{C}\]
Rewrite these equations as
\[I_1-I_2=LC \omega^2 I_1 \]
\[-I_1+2I_2-I_3=LC \omega^2 I_2 =\]
\[-I_2+I_3=LC \omega^2 I_3 =\]
In matrix form this is
\[\left( \begin{array}{ccc} 1 & -1 & 0 \\ -1 & 2 & -1 \\ 0 &-1 & 1 \end{array} \right) \begin{pmatrix}I_1\\I_2\\I_3\end{pmatrix}= \omega^2 LC \begin{pmatrix}I_1\\I_2\\I_3\end{pmatrix}\]
.The natural frequencies of the circuit are the square roots of the eigenvalues.
Solve
\[ det \left( \begin{array}{ccc} 1- \omega^2 LC & -1 & 0 \\ -1 & 2- \omega^2 LC & -1 \\ 0 &-1 & 1- \omega^2 LC \end{array} \right) = \omega^2 LC (\omega^2 LC -1)( \omega^2 LC -3)=0\]
Hence the frequencies of the system are
\[\omega^2 LC=0 \rightarrow \omega =0, \: \omega^2 LC=1 \rightarrow \omega =\sqrt{\frac{1}{LC}}, \: \omega^2 LC=3 \rightarrow \omega =\sqrt{\frac{3}{LC}}\]
. 
