A regular Sturm Liouville equation is a real second-order linear differential equation of the form
![]() with boundary conditions
with boundary conditions![]() with at least one of
with at least one of![]() and similarly for
and similarly for![]() and with the functions
and with the functions![]() specified.
specified.
In the simplest case all coefficients are continuous on the finite closed interval![]() and
and![]() has continuous derivative. In this case, this function
has continuous derivative. In this case, this function![]() is a solution if it is continuously differentiable on
is a solution if it is continuously differentiable on![]() and satisfies (1) at every point in
and satisfies (1) at every point in![]() In addition,
In addition,![]() is typically required to satisfy some boundary conditions at
is typically required to satisfy some boundary conditions at![]() and
and![]() The function
The function![]() is called the weight function.
is called the weight function.
The value of![]() is not specified in the equation; finding the values of
is not specified in the equation; finding the values of![]() for which there exists a non-trivial solution of (1) satisfying the boundary conditions is part of the problem called the Sturm–Liouville problem.
for which there exists a non-trivial solution of (1) satisfying the boundary conditions is part of the problem called the Sturm–Liouville problem.
Such values of![]() when they exist are called the eigenvalues of the boundary value problem defined above and the given boundary conditions. The corresponding solutions (for each
when they exist are called the eigenvalues of the boundary value problem defined above and the given boundary conditions. The corresponding solutions (for each![]() ) are the eigenfunctions of this problem. The solutions (eigenfunctions) of each Sturm - Liouville problem form an orthogonal basis for the set of continuous functions, so that if
) are the eigenfunctions of this problem. The solutions (eigenfunctions) of each Sturm - Liouville problem form an orthogonal basis for the set of continuous functions, so that if![]() and
and![]() are solutions for distinct
are solutions for distinct![]() then
then![]()
We wish to find a function![]() which solves the following Sturm – Liouville problem:
which solves the following Sturm – Liouville problem:
![]() with
with![]()
In fact![]() is a solution with eigenvalue
is a solution with eigenvalue![]()
Properties:
The eigenvalues of Sturm – Liouville problems form an infinite set:![]() with
with ![]() as
as![]()
Any pair of eigenfunctions corresponding to a particular eigenvalue are non – zero multiples of one another.
If![]() is a complete set of eigenfunctions for (1) then
is a complete set of eigenfunctions for (1) then
a) The![]() form a basis for
form a basis for![]() the set of continuous functions with continuous first derivatives.
the set of continuous functions with continuous first derivatives.
b)Let![]() be any function in
be any function in![]() and let
and let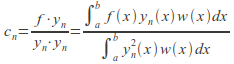 be the nth Fourier coefficient of
be the nth Fourier coefficient of![]() with respect to the basis
with respect to the basis![]() then the Fourier series
then the Fourier series![]() converges pointwise to
converges pointwise to![]() on
on![]()
