\[P(x_P,y_P)\]
is equal to the length of the normal drawn from the point to the \[x\]
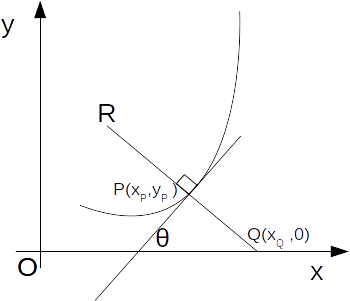
axis. In the diagram,
\[| PQ | = | r | =\frac{(1+ (\frac{dy}{dx})^2)^{3/2}}{ \frac{d^2y}{dx^2}}\]
.
\[(x_P,y_P)\]
is \[y-y_P = -1/ \frac{dy}{dx}_{(x_P,y_P)} (x-x_P)\]
. When \[y=0\]
, \[y_P \frac{dy}{dx}_{(x_P,y_P)}=x_Q-x_P\]
.Hence
\[| PQ | = \sqrt{y_P^2 +(x_Q-x_P)^2}=y_P \sqrt{1+ (\frac{dy}{dx}_{(x_P,y_P)})^2}\]
.\[| PQ | = | r | \rightarrow y_P \sqrt{1+ (\frac{dy}{dx}_{(x_P,y_P)})^2} =\frac{(1+ (\frac{dy}{dx})^2)^{3/2}}{ \frac{d^2y}{dx^2}} \rightarrow y_P | \frac{d^2y}{dx^2}_{(x_P,y_P)} | = 1+(\frac{dy}{dx})^2) \]
. Since \[P\]
is a general point we can write \[y | \frac{d^2y}{dx^2}| = 1+(\frac{dy}{dx})^2) \]
.Suppose
\[\frac{d^2y}{dx^2} \gt 0\]
. Let \[\frac{dy}{dx}=p\]
then can write the last equation as \[1+p^2=yp \frac{dp}{dy} \rightarrow \frac{1}{y}dy= \frac{p}{1+p^2} dp \rightarrow \int \frac{1}{y}dy= \int \frac{p}{1+p^2} dp \rightarrow ln(y)+c = \frac{1}{2} ln(1+p^2)\]
.This can be written as
\[Ay^2=1+p^2= 1+ (\frac{dy}{dx})2 \frac{dy}{dx}=\sqrt{Ay^2-1}\]
.Separating variables and integrating again gives
\[\frac{1}{\sqrt{A}} cos^{-1} y=x+B\]
.Similarly, letting
\[\frac{d^2y}{dx^2} \lt 0\]
and solving gives the equation of a family of circles. 