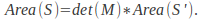In general a matrix operating on a vector may reflect, rotate, shear it, or a combination of these. We can deduce the nature of the transformation by inspection of the matrix.
If the determinant of the matrix is positive, it must be a rotation or a combination of a rotation and a shear.
It the determinant of the matrix is 1 and the columns or rows have length 1 when considered as a vector then it is a rotation. The matrix (in two dimensions) may be written
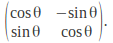 We can find the rotation angle by equating the transformation matrix to this and solving for
We can find the rotation angle by equating the transformation matrix to this and solving for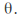 Note that in general two one equation needs to be solved for each of
Note that in general two one equation needs to be solved for each of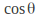 and
and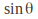 to get the correct answer.
to get the correct answer.If the determinant of the matrix is negative, then it must be either a reflection or a combination of a reflection and a shear.
It the determinant of the matrix is -1 and the columns or rows have length 1 when considered as a vector then it is a reflection. The matrix (in two dimensions) may be written
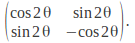 We can find the angle
We can find the angle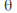 that the reflection line makes with the
that the reflection line makes with the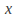 - axis by equating the transformation matrix to this and solving for
- axis by equating the transformation matrix to this and solving for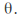 Note that in general two one equation needs to be solved for each of
Note that in general two one equation needs to be solved for each of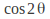 and
and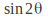 to get the correct answer.
to get the correct answer.If the matrix scales a vector, it may scale in the
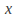 direction or the
direction or the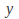 direction or both. If it scales in the
direction or both. If it scales in the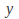 direction only, then it must leave any
direction only, then it must leave any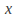 value unchanged, so that if the transformation is represented by
value unchanged, so that if the transformation is represented by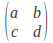 then
then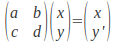 so that
so that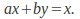 Since
Since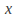 and
and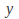 are arbitrary, we must have
are arbitrary, we must have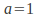 and
and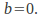 Similarly, if the matrix represents a scaling in the
Similarly, if the matrix represents a scaling in the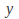 direction only, then
direction only, then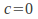 and
and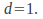 Of course we may multiply matrices representing
Of course we may multiply matrices representing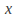 and
and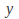 scalings to obtain a matrix that scales in both directions simultaneously.
scalings to obtain a matrix that scales in both directions simultaneously.The area of any shape transformed is related to the area of the untransformed shape by the determinant of the transformation matrix,
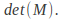 If
If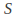 and
and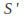 are the original and transformed shapes then
are the original and transformed shapes then