When someone attaches themselves to a piece of elastic and jumps off a bridge, energy initially all gravitational potential energy is changed into kinetic energy as the jumper falls and finally into elastic potential energy as the elastic reaches a maximum length.
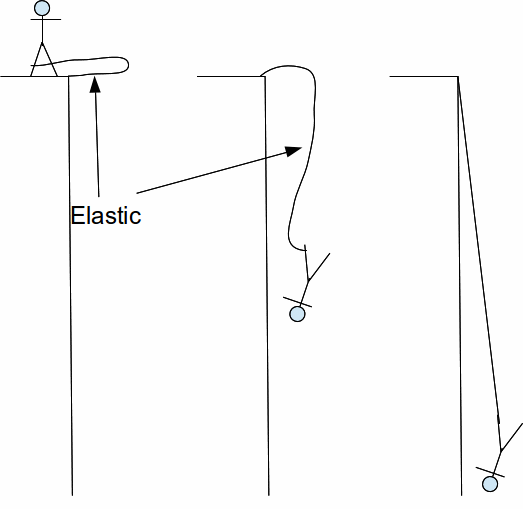
Suppose that the unstretched length of elastic is![]() its modulus of elasticity is
its modulus of elasticity is![]() and the mass of the jumper is
and the mass of the jumper is![]() We want to find the maximum kinetic energy and the maximum extension of the string.
We want to find the maximum kinetic energy and the maximum extension of the string.
Before the jumper jumps we can take gravitational potential energy,![]() equals kinetic energy,
equals kinetic energy,![]() equals elastic potential energy,
equals elastic potential energy,![]() equals 0, so that throughout the motion
equals 0, so that throughout the motion![]()
When the elastic has maximum extension and length![]() the jumper is not moving so his kinetic energy is zero.
the jumper is not moving so his kinetic energy is zero.
Then![]() and the maximum length
and the maximum length![]() is a solution to
is a solution to![]()
This equation has two solutions. Take the one with the positive root. The other will correspond to a height above the jumping point.
The maximum kinetic energy will occur when the tension in the elastic is equal to the force of gravity on the descending jumper:![]() so that
so that![]() Below this point the jumper will start to decelerate.
Below this point the jumper will start to decelerate.
Then![]()
