If samples of size![]() aretaken from a population whose mean
aretaken from a population whose mean![]() andstandard deviation
andstandard deviation![]() isknown then
isknown then![]() themean of the sample has the normal distribution
themean of the sample has the normal distribution![]() Ifwe know the standard deviation but not the mean of the populationthen we can find a confidence interval for the mean of the populationby rearranging
Ifwe know the standard deviation but not the mean of the populationthen we can find a confidence interval for the mean of the populationby rearranging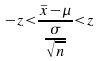 (1)to give
(1)to give![]() (2) with probability corresponding to the value of z. Hence theconfidence interval for the mean is given by
(2) with probability corresponding to the value of z. Hence theconfidence interval for the mean is given by![]() (3)
(3)
Note that confidenceintervals are two sided. If we are required to find a 90% confidenceinterval the we look up that value of z corresponding to aprobability of![]() inthe tables for the normal distribution.
inthe tables for the normal distribution.
In practice, the standard deviation is only one morething to be calculated from the data, so there is rarely such a thingas the 'true' standard deviation![]() Inthe case where the population is normal but the standard deviationhas to be calculated from the sample we cannot use the aboveexpression for the confidence interval. Instead we use student's
Inthe case where the population is normal but the standard deviationhas to be calculated from the sample we cannot use the aboveexpression for the confidence interval. Instead we use student's![]() –distribution. The
–distribution. The![]() –distribution is similar to the normal distribution, beingsymmetrical, bell shaped and having most most values occurring withinthree or so standard deviations from the mean. In addition as
–distribution is similar to the normal distribution, beingsymmetrical, bell shaped and having most most values occurring withinthree or so standard deviations from the mean. In addition as![]() the
the![]() –distribution approximates more closely to the normal distribution.
–distribution approximates more closely to the normal distribution.
If![]() isthe standard deviation calculated from the sample of size
isthe standard deviation calculated from the sample of size![]() theninstead of (1) we have
theninstead of (1) we have 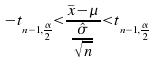 andinstead of (2) we have
andinstead of (2) we have 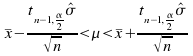 and (3) becomes
and (3) becomes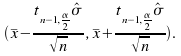
Example: Find a 95 %confidence interval for the meanof the population from which the following sample is taken, assumingthat the population is normally distributed.
3,4,3,4,5,6,2,3,4,5
![]()
![]()
![]() fromthe tables.
fromthe tables.
The confidence interval is![]()
