\[m_1\]
and \[m_2\]
with \[m_1 \gt m_2\]
then the angle between the lines is \[tan^{-1} (m_1) - tan^{-1}(m_2)\]
.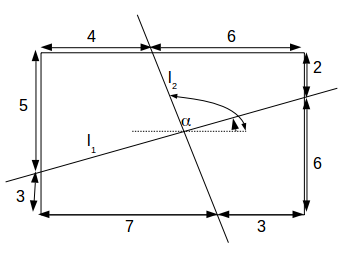
\[l_1\]
goes along 7+3=10 and up 6-3=3. The gradient is \[\frac{3}{10}\]
.The line
\[l_2\]
goes along 3-6=-3 and up 3+5=8. The gradient is \[\frac{8}{-3}\]
.The angle
\[\alpha\]
is \[tan^{-1}( \frac{8}{-})- tan^{-1}(\frac{3}{10})=93.9^o\]
to 1 decimal place.
