Definition: If A is at position![]() moving with velocity
moving with velocity![]() and B is at position
and B is at position![]() moving with velocity
moving with velocity![]() then
then
-
The relative position of B relative to A is given by
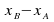 and the relative velocity of B relative to A is given by
and the relative velocity of B relative to A is given by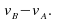
-
The relative position of A relative to B is given by
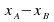 and the relative velocity of A relative to B is given by
and the relative velocity of A relative to B is given by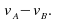
-
The position of
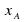 of A at any time t is given by
of A at any time t is given by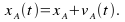
-
The position of
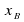 of B at any time t is given by
of B at any time t is given by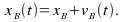
Typically we are are asked about relative velocities, relative positions and points of intersection or CRASHES!
Example A boat A started from position![]() with speed
with speed![]() .
.
a)Find the position of A at time t
![]()
If boat B start from position![]() with velocity
with velocity![]() find if boat A and B CRASH and if they do, find the position of the crash site and the distance from the origin to this position.
find if boat A and B CRASH and if they do, find the position of the crash site and the distance from the origin to this position.
The position vector of B at time t is given by![]()
If they collide, at some point they are in the same place at the same time. This means that for some value of![]() We solve:
We solve:
![]()
We equate the coefficients of![]() and
and![]() on both sides:
on both sides:
![]()
![]()
We get the same value of t from both equations hence they meet at the same place at the same time.
We can obtain the position vector of the point of collision be substituting the value t=2 into either![]() or
or![]()
![]()
![]()
The distance from the origin to![]() is given by
is given by![]() so distance from origin to crash site is
so distance from origin to crash site is![]()
