\[r\]
?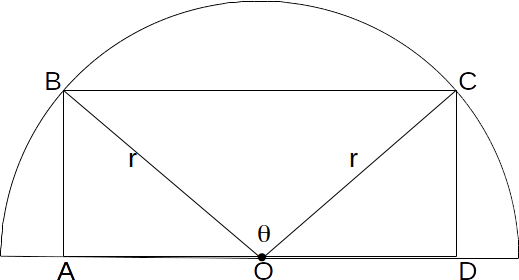 Let the triangle OBC subtend an angle
Let the triangle OBC subtend an angle \[\theta\]
at the centre of the circle.The triangles ABO abd CDO have the same area by symmetry, and together subtend an angle of
\[\pi - \theta\]
. We can consider them to form a triangle with sides \[r\]
from the centre of the circle to the edge, and subtending an angle of \[\pi - \theta\]
at the centre.The area of the rectangle is then
\[\begin{equation} \begin{aligned} \frac{1}{2} r^2 sin \theta + \frac{1}{2} sin (\pi - \theta) &= \frac{1}{2} r^2 (sin \theta + sin (\pi - \theta )) \\ &= \frac{1}{2}r^2( sin \theta + sin \theta ) \\ &= r^2 sin \theta \end{aligned} \end{equation}\]
The maximum value of
\[sin \theta\]
is 1, when \[\theta = \frac{ \pi}{2}\]
so the maximum area of the rectangle is \[r^2\]
. 