\[y=16-x^2\]
and the \[x\]
axis?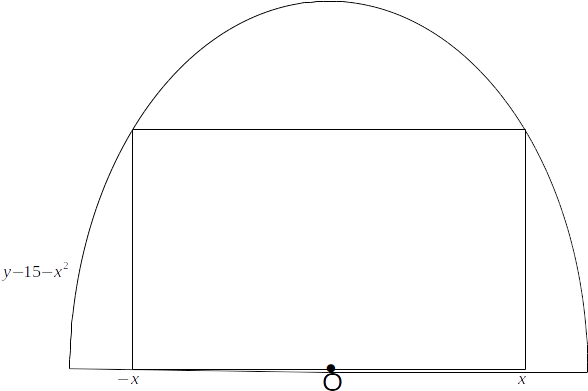 From the diagram, the base of the rectangle is
From the diagram, the base of the rectangle is \[3x\]
and the height is \[16-x^2\]
os the area is \[A=x(16-x^2)=16x-x^3\]
.\[\frac{dA}{dx}=16-3x^2\]
.Set
\[\frac{dA}{dx}=0\]
and solve to give \[x= \frac{4 \sqrt{3}}{3}\]
.The area is then
\[A=16 \frac{4 \sqrt{3}}{3} - (\frac{4 \sqrt{3}}{3})^3= \frac{128 \sqrt{3}}{9}\]
. 