Given a function![]() we can easily find a value of
we can easily find a value of![]() given a value of
given a value of![]() by substituting the value of
by substituting the value of![]() into the function
into the function![]() If however we want to find the value of
If however we want to find the value of![]() given a value of
given a value of![]() then at some stage we will have to either invert the function or solve an equation to find
then at some stage we will have to either invert the function or solve an equation to find![]() The first method is usually preferable because it is general: in inverted function means we can find any value of
The first method is usually preferable because it is general: in inverted function means we can find any value of![]() given a value of
given a value of![]()
There are three steps to inverting a function![]()
1. Make![]() the subject so that you have another function
the subject so that you have another function![]()
-
Interchange occurrencesof
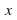 and
and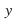 sono you have
sono you have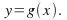
-
Replace
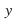 by
by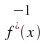 :the answer is
:the answer is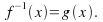
Example:
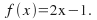 Find
Find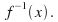
-
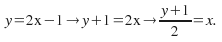
-
Interchange
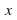 and
and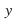 :
: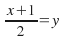
-
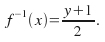
If you draw the graphs of
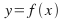 and
and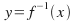 on the same axis you will notice something very striking. The line
on the same axis you will notice something very striking. The line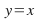 is a line of symmetry: to obtain the graph
is a line of symmetry: to obtain the graph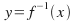 just reflect the graph
just reflect the graph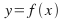 in the
in the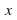 – axis. To see why this is so, notice that steps 1 and 2 above interchange
– axis. To see why this is so, notice that steps 1 and 2 above interchange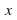 and
and
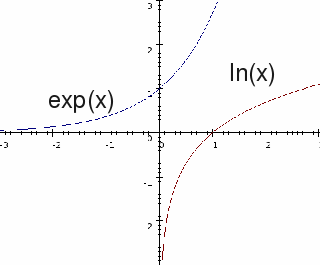
This is illustrated above for the graphs
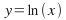 and
and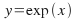 which are inverse to each other.
which are inverse to each other.A problem may arise if you have a function
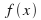 which gives the same value of
which gives the same value of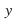 for more than one value of
for more than one value of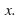 When you try to invert the function and you find
When you try to invert the function and you find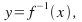 a value of
a value of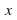 may return no value of
may return no value of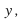 or more than one value of
or more than one value of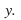 It is necessary in a case like this to restrict the domain of the inverse function to eliminate those “impossible”
It is necessary in a case like this to restrict the domain of the inverse function to eliminate those “impossible”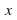 's and “duplicate”
's and “duplicate”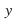 's. For example, if
's. For example, if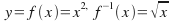 – we take the positive square root to ensure only one value of
– we take the positive square root to ensure only one value of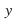 for each value of
for each value of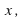 and we must have
and we must have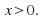 If
If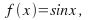 then
then 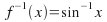 and the domain of
and the domain of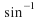 is
is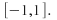 We take the range to be
We take the range to be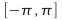 so that there is one value of
so that there is one value of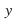 for each
for each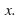
-
