Not all sequences either always converge or always diverge. Often a series converges for some values of
and diverges for other values of
If a function is expanded in a power series about a point
so that
then the set of values ofabout
for which the series converges is called the interval of convergence and if the series converges for all
and diverges for all
then
is the radius of convergence.
The interval of convergence can often be found using the ratio test with the condition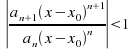
or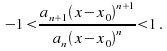 
Example: find the interval of convergence for the power series
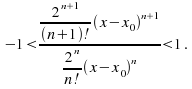
Cancellation gives
Allowing
now shows that interval of convergence is
Example: find the interval of convergence for the power series
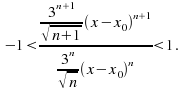
Cancellation gives
Let then
The radius of convergence is
and the interval of convergence is