Basically, Fourier series express a function as a sum of sine or cosine terms. They are useful because many differential equations are linear, so that if![]() and
and![]() are solutions to the equation then so is
are solutions to the equation then so is![]() for suitable
for suitable![]() and
and![]() and by extension, any linear combination of solutions is also a solutions, with suitable coefficient
and by extension, any linear combination of solutions is also a solutions, with suitable coefficient![]() Expressing a function as a sum of sine and cosine terms is especially useful because many wavefunctions are naturally expressed in terms of linear combinations of sine and cosine terms.
Expressing a function as a sum of sine and cosine terms is especially useful because many wavefunctions are naturally expressed in terms of linear combinations of sine and cosine terms.
Any continuous function defined on an interval can be expressed as a Fourier series, and any function with a finite number of discontinuities. The function is extended outside the range on which it is defined by defining it as a repeating function, because sin and cosine are repeating functions with period![]() so for example, if
so for example, if
![]()
Then we can extend![]() outside the interval
outside the interval![]() by writing
by writing![]() where
where![]()
This is illustrated below.
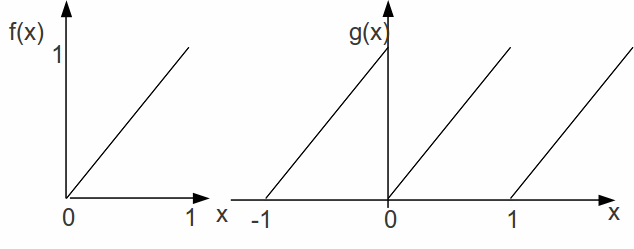
In general for![]() We can extend
We can extend![]() outside the interval by writing
outside the interval by writing![]()
We can in fact extend a function in more than one way, besides the sample given above. We can extend![]() to be an even function, so that
to be an even function, so that![]()
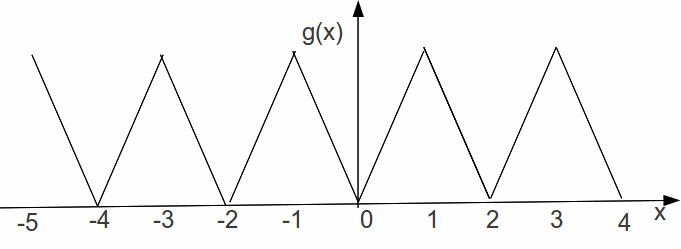
or we can extend![]() to be an odd function, so that
to be an odd function, so that![]() while maintaining periodicity.
while maintaining periodicity.
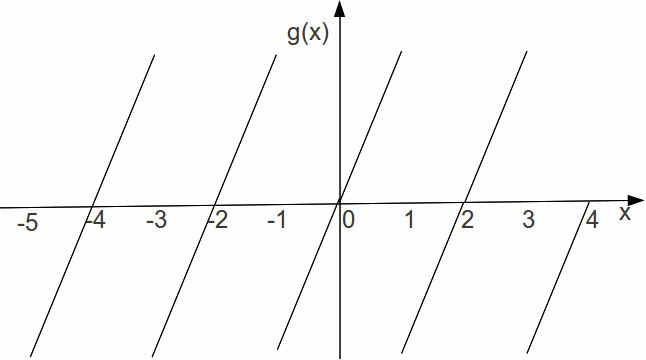
For these two extensions the period has doubled, but periodicity remains.
