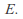Weierstrass's M – test provides a way to prove uniform convergence for the sum of a sequence.
Let![]() be a sequence of functions on a set
be a sequence of functions on a set![]() and suppose that there is a sequence of positive terms
and suppose that there is a sequence of positive terms![]() such that
such that
-
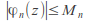 for
for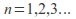 and all
and all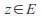
-
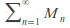 is convergent
is convergentThen the series
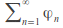 is uniformly convergent on
is uniformly convergent on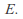
Proof: Note that by assumption 1 and 2,
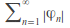 is convergent for each
is convergent for each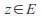 by the comparison test. hence
by the comparison test. hence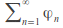 is convergent for each
is convergent for each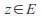 by the absolute convergence test and so the sum function
by the absolute convergence test and so the sum function exists for each
exists for each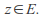 We note the partial sum functions by
We note the partial sum functions by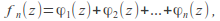
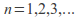
Then for
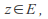
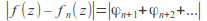
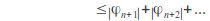 by the triangle inequality
by the triangle inequality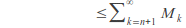 by assumption 1
by assumption 1By assumption 2,
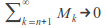 as
as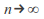 so uniform convergence follows..
so uniform convergence follows..Example: Prove that
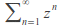 converges uniformly on
converges uniformly on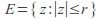 for
for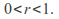
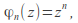
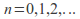
and
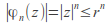 for
for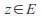
so that assumption 1 above is satisfied with
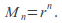
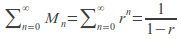 for
for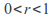
so that assumption 2 is satisfied and the sum converges uniformly on