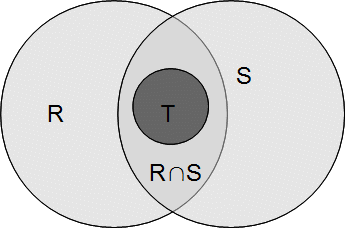
We start with a
Definition Let
and
be analytic functions whose domains are the regions
and
respectively.andare direct analytic continuations of each other if there is a region
such that
for
Example:
is only defined for
but we may write
on the region defined by
but
is defined on the wider region
is an analytic continuation of
Example:
is normally defined on the region
so that
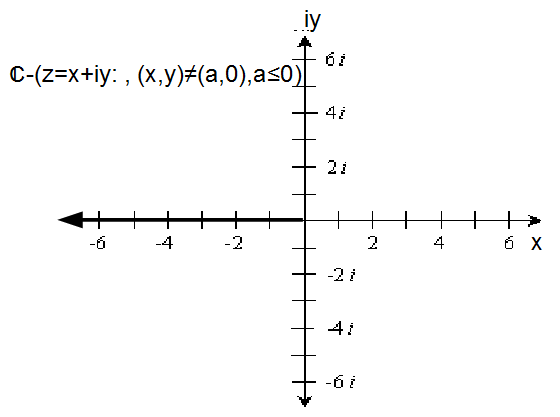
We in fact only need Log to be one to one on the complex plane so that the inverse is defined. We can instead define Log-1 z on
so that
for
and we have extended
to be defined on