Compact, Open, Closed and Bounded Sets

A closed setis a set that includes all it's limit points

This means than for each pointsuch that there exists a sequencesuch thatwe must have that

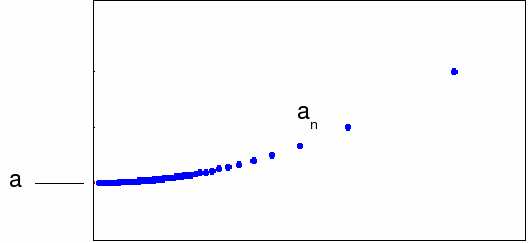
This means that the boundary ofis in

If the set does not include any of it's boundary then it is said to be open. The intervalis closed, and the intervalis open since the boundary ofisbutThe intervalis neither open or closed sincebut

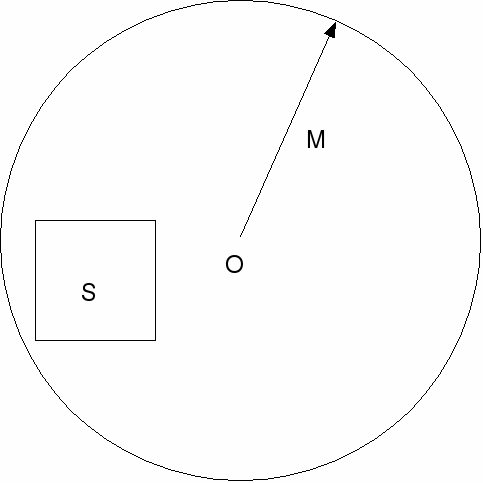
A setis bounded if and only if there existssuch that for allThis means that the distance however measured from the origin to any element ofis less than or equal toas shown below.

Finally a set is compact if it is both closed and bounded. Compactness has many applications in analysis.