Not all sequences either always converge or always diverge. Often a series converges for some values of![]() and diverges for other values of
and diverges for other values of![]()
If a function is expanded in a power series about a point![]() so that
so that![]() then the set of values of
then the set of values of![]() about
about![]() for which the series converges is called the interval of convergence and if the series converges for all
for which the series converges is called the interval of convergence and if the series converges for all![]() and diverges for all
and diverges for all![]() then
then![]() is the radius of convergence.
is the radius of convergence.
The interval of convergence can often be found using the ratio test with the condition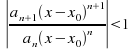 or
or 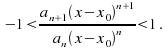
Example: find the interval of convergence for the power series![]()
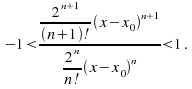
Cancellation gives![]() Allowing
Allowing![]() now shows that interval of convergence is
now shows that interval of convergence is![]()
Example: find the interval of convergence for the power series![]()
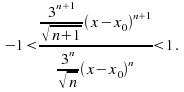
Cancellation gives![]() Let
Let![]() then
then![]()
The radius of convergence is![]() and the interval of convergence is
and the interval of convergence is![]()
