Continuous Functions on Compact Sets

Continuous functions preserve some properties of the sets on which they operate. One of the most important of these preserved properties is compactness.

Theorem

If a continuous functionoperates on a closed and bounded – compact – setthen the imageis also closed and bounded or compact.

Proof

By the extreme value theorem,is bounded. If we can prove thatis open, then we have proved thatis closed. Since it is also bounded it is compact.

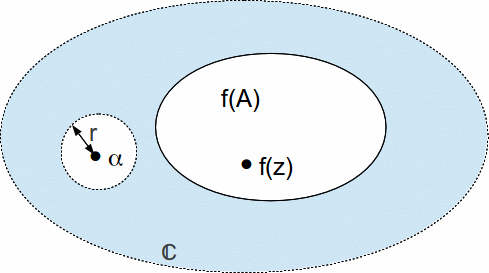
Suppose therefore, thatWe want to find an open disc centred atlying entirely inConsiderwhich is non – zero onsincefor and is continuous on

By the extreme value theorem there existssuch that

for all

that is

for all

whereso the open disc with centreand radiuslies entirely insois compact.