Existence and Uniqueness of Inverse Points With Respect to a Generalized Circle

Ifis a generalized circle andis an arbitrary point of the extended complex planethenhas a unique inverse pointwith respect to

Proof

Ifthen we may takesince any point onis inverse to itself. If letbe the extended line throughthat meetsat right angles at the point

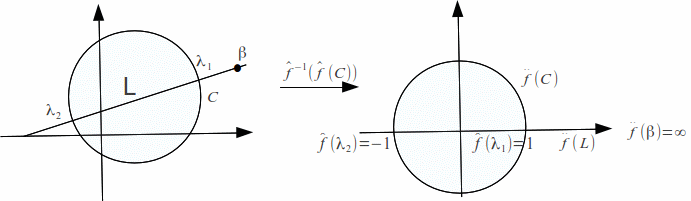
In either case letbe the extended mobius transformation that mapstoto 1 andto -1 thenis the extended real axis and it meetsatandFurthermoremeetsat right angles atsince preserves angles. sois the unit circle. Ifthenandso andare inverse points with respect toThe existence of inverse points is proved.

To prove uniqueness, ifandare unique points with respect tothenand somust be unique.