When finding a Laurent series it is important to specify the region on which the series is to converge. The function
is analytic on each of
and
The Laurent series on each of the above regions is not the same however.
To find the Laurent series, start by writing
in terms of its partial fractions.
To find the Laurent series on
expand each term about
using the binomial theorem.
The first series below will converge for
and the second will converge forso the sum will converge for
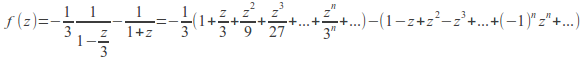
To find the Laurent series on
use the expansion above for
valid for and write
so that the binomial expansion will converge for
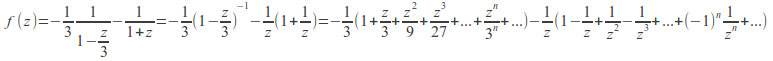
To find the Laurent series on
write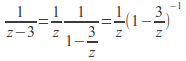
valid for and write
so that the binomial expansion will converge for
and the sum will converge for
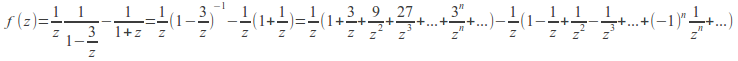
