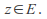A sequence of functions converges uniformly to a function![]() on a set
on a set![]() if for each
if for each![]() there is an integer
there is an integer![]() such that for
such that for![]() for all
for all![]() and
and![]()
We say that![]() is uniformly convergent on
is uniformly convergent on![]() with limit function
with limit function![]() It is important to note that
It is important to note that![]() may depend on
may depend on![]() Uniform convergence is illustrated below.
Uniform convergence is illustrated below.
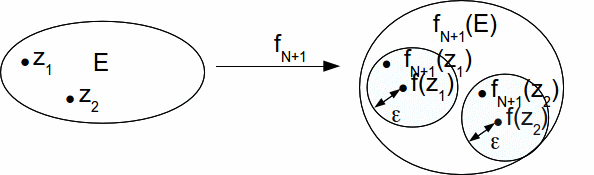
Example: Prove that the complex function![]() converges uniformly on
converges uniformly on![]() to the function
to the function![]()
For each![]()
![]() so
so![]() as
as![]()
Moreover![]()
Choose![]() so that
so that![]() for n>N and clearly
for n>N and clearly![]()
Hence![]() converges uniformly to f on E.
converges uniformly to f on E.
This example illustrates a strategy for proving uniform convergence.
-
Determine the limit function f by evaluating
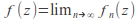 for
for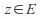
-
Find a null sequence
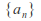 of positive terms such that
of positive terms such that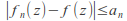 for
for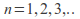 and all
and all