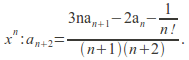Many differential equations do not have analytical solutions – solutions expressed in terms of elementary functions. In these circumstances, a numerical solution must be found. One possible numerical solution is in terms of a series expansion.
To find the series expansion we assume a solution of the form
and substitute into the differential equation, collecting together and equating powers of
If there are any elementary functions in the equation, these are also expanded in powers ofThe solution is then found iteratively using the boundary or initial condition(s). If there is one condition,
or 
then
or
respectively is found first, then the other
found by iteration. For higher order differential equations, equations in themust be formed and solved then the otherfound by iteration.
Example: Solve
with
and
Assume a series solution of the form
then
and
The equation to be solved becomes
We have to collect like powers of
but must first re - index the summations so that
and 
become
To do this write
The equation becomes
We can take all the summations inside a single summation to give
Equate each coefficient of
to zero, since the right hand side is zero.
But
and
so
and
The solution is
with higher order terms defined with a recurrence relation in terms of coefficients of
Example
withand
Assume a series solution of the formthenandThe equation to be solved becomes
We have to collect like powers ofbut must first re - index the summations so thatand becomeTo do this write
The equation becomes
We can take all the summations inside a single summation to give
Equate each coefficient ofto zero, since the right hand side is zero.
Butandso
and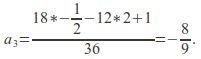
The solution is
with higher order terms defined with a recurrence relation in terms of coefficients of