\[x=a( \theta- sin \: \theta ) , \: y=a(1- cos \: \theta )\]
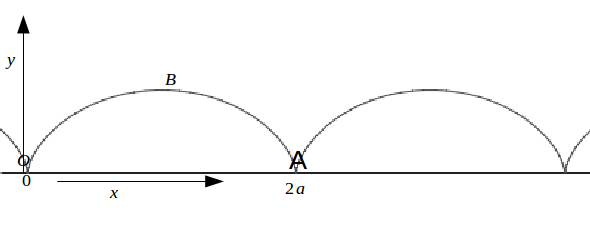
\[\begin{equation} \begin{aligned} A &= \frac{1}{2} \oint x \: dy - y \:dx \\ &=\frac{1}{2} \int_{OA+ABO} x \: dy - y \:dx \\ &= \frac{1}{2} \int_{ABO} x \: dy - y \:dx \\ &= \frac{1}{2} \int a(\theta - sin \: \theta )a \: sin \: \theta -a(1- cos \: \theta ) a(1- \: cos \:theta )d \theta \\ &= \frac{a^2}{2} \int^0_{2 \pi } \theta \: sin \theta + 2 cos \theta -2 d \theta \\ &=\frac{a^2}{2} [- \theta cos \: \theta +3 sin \theta -2 \theta ]^0_{2 \pi} \\ &= 2 \pi a^2 \end{aligned} \end{equation}\]
