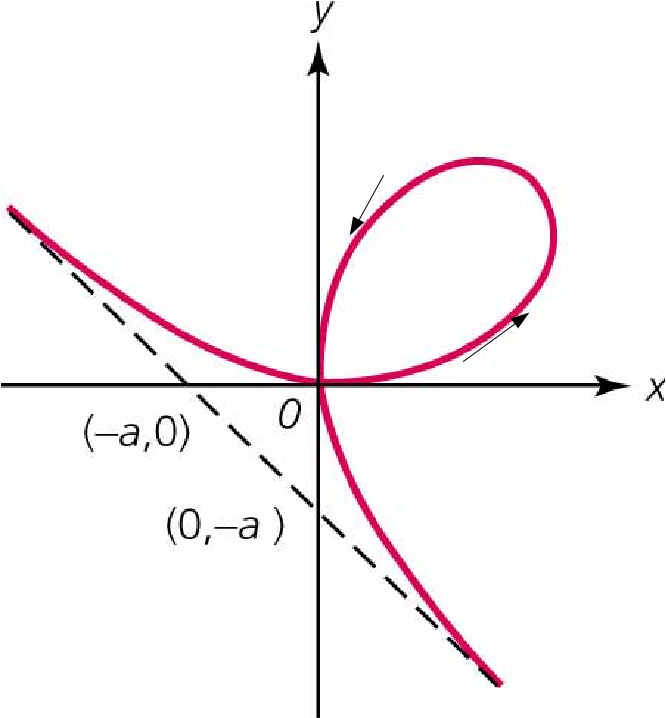
\[x^3 +y^3 =3axy\]
, with \[a>0\]
.
\[y=px\]
to obtain \[x^3 + p^3 ax^23 = 3 p x^2 \rightarrow x= \frac{3ap}{1+p^3}\]
The loop starts at
\[x=y=p=0\]
and when p=1, \[x=y=\frac{3a}{2}\]
As
\[p \rightarrow \infty\]
the line approaches the origin along the positive \[y\]
axis.Green's equation gives
\[\begin{equation} \begin{aligned} A &= \frac{1}{2} \oint_C x \: dy - y \: dx \\ &= \frac{1}{2} \oint_C x \: (p \: dx + x \: dp - y \: dx \\ &= \frac{1}{2} \oint_C x^2 \: dp \\ &=\frac{1}{2} \int^{\infty}_0 \frac{9a^2 p^2}{(1+p^3)^2} \: dp \\ &=9 a^2 \frac{1}{2} \int^{\infty}_0 \frac{ p^2}{(1+p^3)^2} \: dp \\ &= \frac{9 a^2}{2} \int^{\infty}_0 \frac{d}{dp} (- \frac{ 1}{3(1+p^3)}) dp \\ &= 9a^2 [- \frac{1}{3 (1+p^3) }]^{\infty}_0 \\ &= \frac{3a^2}{2} \end{aligned} \end{equation}\]
