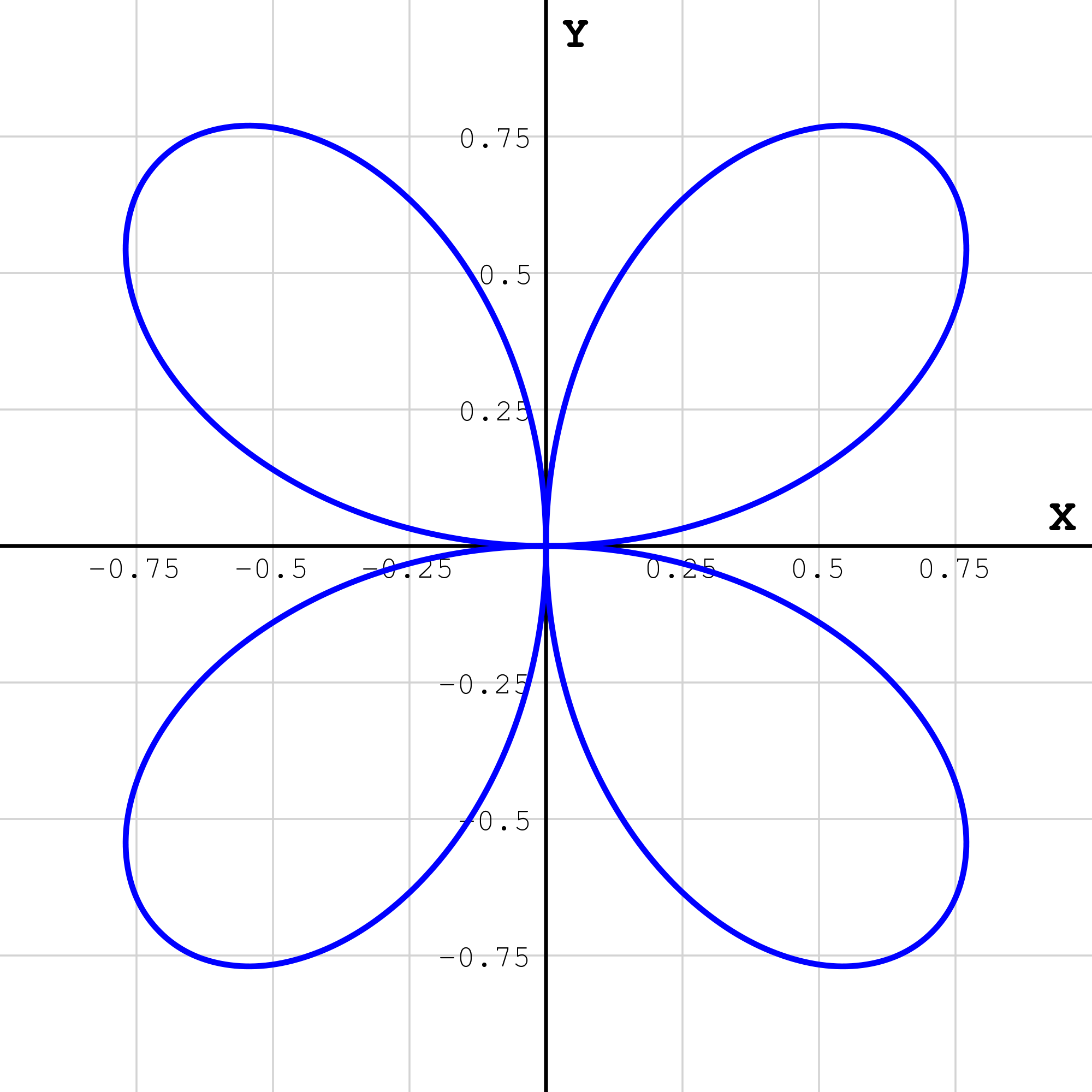
\[r=sin \: 2 \theta\]
.
\[A= \frac{1}{2} \oint r^2 \: d \theta\]
Hence the area enclosed by the outline of a leaf of a four leaf rose is
\[\begin{equation} \begin{aligned} A &= \frac{1}{2} \int^{ \pi /2}_0 r^2 d \theta \\ &= \frac{1}{2} \int^{ \pi /2}_0 sin^2 \: 2 \theta d \theta \\ &= \frac{1}{2} \int^{ \pi /2}_0 \frac{1}{2} - \frac{ cos \: 2 \theta}{2} d \theta \\ &= \frac{1}{2} [ \frac{ \theta}{2} - \frac{ sin \: 2 \theta}{4}]^{ \pi /2}_0 \\ &= \frac{1}{2} (( \frac{\pi}{4} -0-(0-0)) \\ &= \frac{\pi}{8} \end{aligned} \end{equation}\]
