Vertical Point of Inflexion
\[y=f(x)\]
is a vertical point of inflexion if \[\]
if \[\frac{dx}{dy}= \frac{d^2 x}{dy^2}=0\]
or equivalently \[\frac{dy}{dx}= \frac{d^2 y}{dx^2}= \infty\]
.If
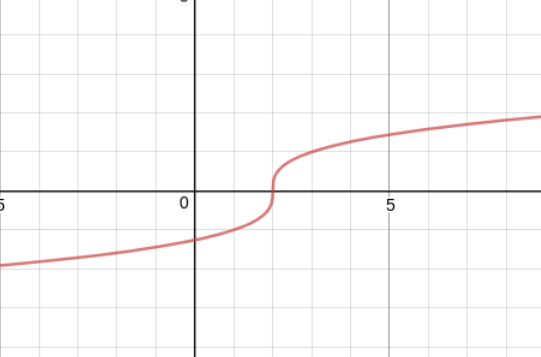
\[y=(x-2)^{1/3}\]
then \[\frac{dy}{dx}=\frac{1}{3}(x-2)^{-2/3}, \; \frac{d^2y}{dx^2}=- \frac{2}{9}(x-2)^{-5/3}\]
.When
\[x=2\]
, \[\frac{dy}{dx}= \frac{d^2y}{dx^2}= \infty\]
so \[x=2\]
is a vertical point of inflexion.
