\[dV=r^2sin \theta d \phi d \theta dr\]
where \[0 \le 0 \phi \lt 2 \pi\]
is the anticlockwise angle from the positive \[x\]
axis to a line drawn from the origin to the projection of a point onto the \[xy\]
plane and \[0 \le \theta \le \pi\]
is the angle from the positive \[z\]
axis to a line drawn to the point.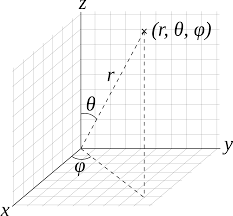
\[r\]
is\[\begin{equation} \begin{aligned} V &= \int^{2 \pi}_0 \int^{\pi}_0 \int^r_0 r^2 sin \theta dr d \theta d \phi \\ &= \int^{2 \pi}_0 \int^{\pi}_0 \int^r_0 [ \frac{r^3}{3} sin \theta]^r_0 d \theta d \phi \\ &= \int^{2 \pi}_0 \int^{\pi}_0 \frac{r^3}{3} sin \theta d \theta d \phi \\ &= \int^{2 \pi}_0 [ \frac{r^3}{3} (-cos \theta) ]^{\pi}_0 d \phi \\ &= \int^{2 \pi}_0 2\frac{r^3}{3} d \phi \\ &= [2\frac{r^3}{3}]^{2 \pi}_0 \\ &= \frac{4}{3} \pi r^3 \end{aligned} \end{equation}\]
