The Cylindrical Coordinate System

We need three number to define a point in three dimensional space, but ordinary Cartesian coordinates with mutually perpendicular axes is not always the best system to use. One alternative is the system of cylindrical coordinates, shown below

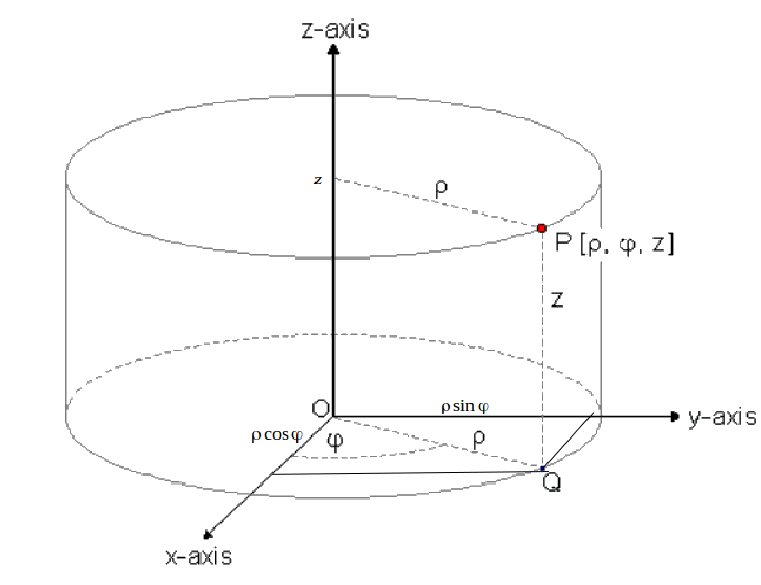
We can write P in any coordinate system. In the Euclidean system we resolve the radial vector from the origin to the point P onto each coordinate axis.
We get