\[(x,y,z)\]
of a point given in spherical coordinates \[(r, , \theta , \phi )\]
are\[x= r cos \phi sin \theta\]
\[y= r sin \phi sin \theta\]
\[z= r cos \theta\]
In cylindrical coordinates
\[( \rho , \phi , z)\]
this becomes\[x= \rho cos \phi\]
\[y= \rho sin \phi \]
\[z= z\]
Since
\[r= \sqrt{X^2 +y^2 +z^2} \]
and \[\rho= \sqrt{X^2 +y^2} \]
we can write \[r= \sqrt{\rho^2 +z^2} \]
\[\phi \]
plays the same role in cylindrical and spherical coordinate systems, and from the diagram below,
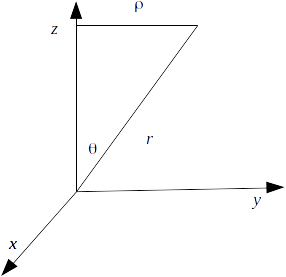
\[\theta = tan^{-1} ( \rho /z) \]
Also
\[dr = \frac{ \rho}{\sqrt{\rho^2 + z^2}} d \rho + \frac{ z}{\sqrt{\rho^2 + z^2}} dz\]
\[dz=dz dz\]
\[\begin{equation} \begin{aligned} \theta &= tan^{-1} (\rho /z) \rightarrow tan \theta = \rho /z \rightarrow d \theta \theta sec^2 \theta =\frac{1}{z} d \rho - \frac{rho}{z^2} dz \\ & d \theta (1+tan^2 \theta ) =\frac{1}{z} d \rho - \frac{rho}{z^2} dz \rightarrow d \theta (1 + \rho /z) =\frac{1}{z} d \rho - \frac{rho}{z^2} dz \\ & d \theta (z^2 + \rho^2) \rightarrow d \theta = \frac{z}{\rho^2 + z%2} d \rho - \frac{\rho}{\rho^2 +z^2} dz \end{aligned} \end{equation} \]
The transformation is
\[ \begin{pmatrix}dr \\ d \theta \\ d \phi \end{pmatrix} = \left( \begin{array}{ccc} \frac{ \rho}{\sqrt{\rho^2 + z^2}} & 0 & \frac{ z}{\sqrt{\rho^2 + z^2}} \\ \frac{z}{\rho^2 + z%2} & 0 & - \frac{\rho}{\rho^2 +z^2} \\ 0 & 1 & 0 \end{array} \right) \begin{pmatrix}d \rho \\ d \phi \\ dz \end{pmatrix} \]
