Transforming functions is related to the transformation of graphs. A function is basically a sequences of operations on some argument. The argument can be anything, but whatever the argument is, the function does the same sequence of operations, in th same order, to each argument. Suppose that the function f says, 'square the argument'.
We can also write
where it is understood that
is the argument.
For this example,
Suppose now that the argument is notbut some other expression in
say
says 'square 3x+1
so that
This definition of a function is precisely consistent with the transformation of a graph. Continuing with the example above,
suppose we replace the argumentby
so that
If we were to transform the graph of
to obtain the graph of
we would scale the– axis by a factor of
When we transform a function however, instead of labelling the x – axis as the x – axis, we label it as theaxis. To relabel it the– axis, we have to divide all the– values on the axis by 2 which is the same as scaling by a factor of
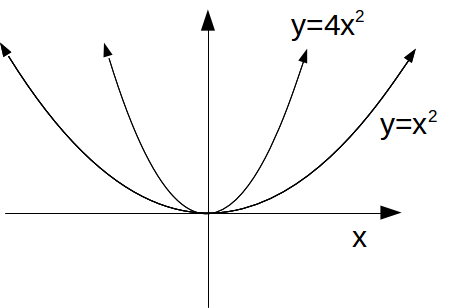
In general, when transforming a function by changing the argument, we can just relabel the– axis. To maintain the– axis as the– axis, we are required to perform the inverse sequence of operations that turned into '' or '
' or whatever the new argument is.