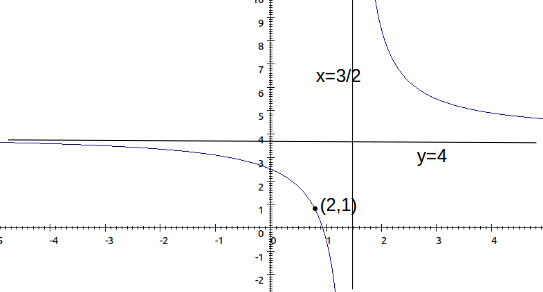
\[x=\frac{3}{2}, \: y=4\]
and passes through the point \[(2,1)\]
.How can we find the equation of the asymptote?
\[(x-x_0)(y-y_0)=k\]
where \[x=x_0, \: y=y_0\]
are the equations of the hyperbolae and \[k\]
is a constant.Hence we can write
\[(x- \frac{3}{2})(y-4)=k\]
.To find the value of
\[k\]
substitute the equation of a point on the curve.\[((2- \frac{3}{2})(1-4)=k \rightarrow k=- \frac{3}{2}\]
.The equation of the hyperbola is
\[(x- \frac{3}{2})(y-4)=- \frac{3}{2}\]
.We can write this as
\[y-4=\frac{-3/2}{x-3/2} \rightarrow y= \frac{-3/2}{x-3/2} +4=\frac{-3/2+4(x-3/2)}{x-3/2}=\frac{4x-15/2}{x-3/2}=\frac{8x-15}{2x-3}\]
We can write this as
\[y-4=\frac{-3/2}{x-3/2} \rightarrow y= \frac{-3/2}{x-3/2} +4=\frac{-3/2+4(x-3/2)}{x-3/2}=\frac{4x-15/2}{x-3/2}=\frac{8x-15}{2x-3}\]
