\[f(x)=\frac{p(x)}{q(x)}\]
where \[p(x), \: q(x)\]
are polynomials.We can find the asymptotes by analysing
1. The zeros of
\[q(x)\]
.2. The behaviour of
\[\frac{p(x)}{q(x)}\]
as \[x \rightarrow \infty\]
and \[x \rightarrow - \infty\]
.Example:
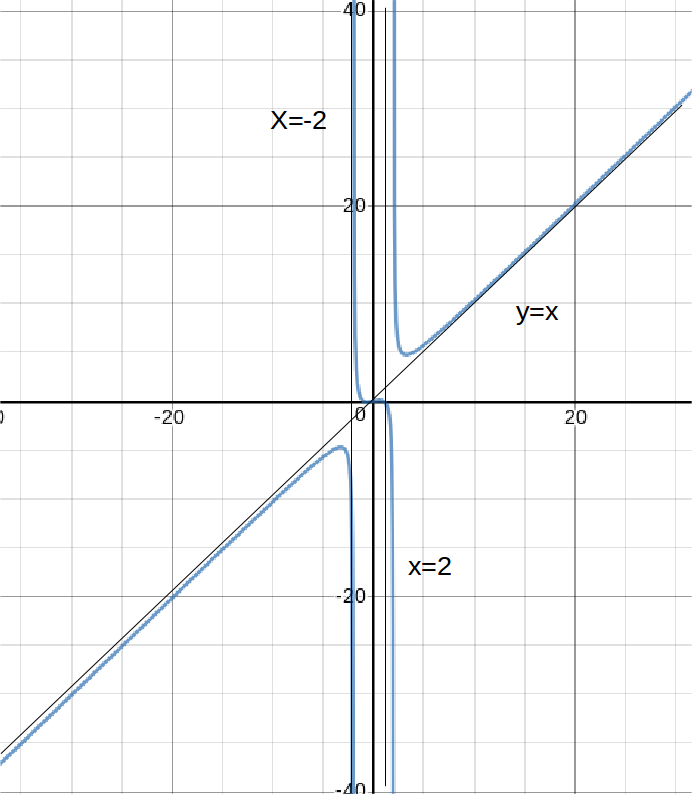
\[f(x)=\frac{x^3-x}{x^2-4}\]
.The denominator
\[x^2-4=(x+2)(x-2)\]
has zeros and asymptotes at \[x=-2, \: x=2\]
.As
\[x \rightarrow \infty\]
, \[lim_{x \rightarrow \infty} f(x)= lim_{x \rightarrow \infty} \frac{x^3-x}{x^2-4} =lim_{x \rightarrow \infty} \frac{x-x/x^2}{1-4/x^2}=x\]
. ,/P>
,/P>
