The safest way to solve absolute value equations for real numbers is to sketch the functions and label each section of each graph with a function. Any solutions can then be visualised and it is easy to see if a solution exists or does not. Example: Solve
\[|x|=2|x-2|-1 \]
.
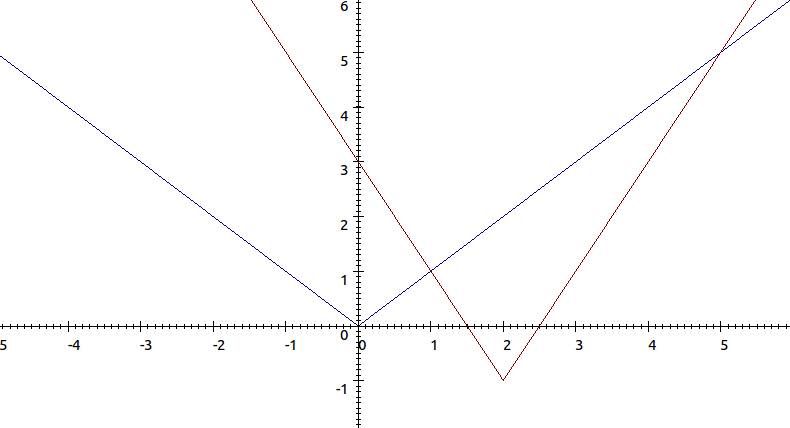
When we remove the modulus sign from an expression we can apply a
\[+\]
or a \[-\]
option. Apply the \[+\]
option to any section of graph going up and the \[-\]
option to any section of graph going down/ For the graph \[2|x-2|-1 \]
we obtain \[2(x-2)-12x-5\]
and \[2(-(x-2))-1=-2x+3 \]
.We get
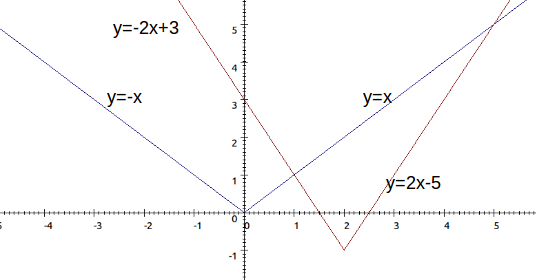
Now solve.
\[x=2x-5 \rightarrow x=5\]
\[x=-2x+3 \rightarrow 3x=3 \rightarrow x=1\]
